/ Články / Matematika / Klasický problém šatnářky

Klasický problém šatnářky

Pánové přijdou do divadla a odloží své klobouky do šatny. Při odchodu šatnářka každému vydá právě jeden klobouk. Jaká je pravděpodobnost, že žádný z pánů nedostane při odchodu svůj klobouk? Předpokládejme, že nikdo z pánů nebude reklamovat přidělený klobouk.
Autor: Jaroslav Dufek

Řešení:

Očíslujme příchozí a jejich klobouky {1,…,n}, potom náhodné vydávaní klobouků odpovídá náhodné permutaci π množiny {1,…,n}, π(i) je číslo vráceného klobouku i-tému pánovi. Naším cílem je zjistit pravděpodobnost, že vzorecOznačme πS(n) pro které předchozí podmínka splněna, protože šatnářka vydává klobouky náhodně jsou všechny n! permutace stejné pravděpodobné a tudíž hledaná pravděpodobnost odpovídá zlomku Vzorec.

Sjednocením všech množin Ai={π ϵ Sn; π(i)=i}, kde Sn je množina všech permutací množiny {1,…,n}, tj. množin které obsahují permutaci s alespoň jedním pevným bodem, dostaneme všechny nevyhovující permutace. Dále |Ai|=n-1, protože π(i) je fixováno a ostatní jsou libovolné.

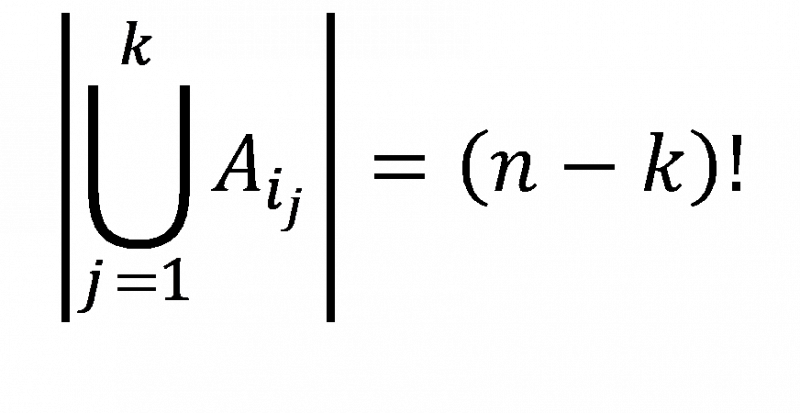Potom pro vzorecplatívzoreca po aplikaci principu inkluze a exkluze dostaneme

vzorec

Potom počet všech permutací bez pevného bodu je roven počtu všech permutací mínus počet permutací s alespoň jedním pevným bodem, tedy

vzorec

potom výsledná pravděpodobnost je

vzorec

Tedy hledaná pravděpodobnost se blíží velikosti e-1.

Poznámka: limitní konvergence je velmi rychlá tj. již pro n=7.